Page Views: 1825
Big O is a way to categorize your algoithms time or memory usage based on the input
As your input grows Big O shows how fast your computation or memory grows.
Using Big O can help you make decisions on whether or not to use certain algoithms.
func sum(num array) int {
sum := 0
for (i = 0; i < num.length; i++) {
sum += n;
}
return sum
}In the example our function grows based on the length of the number
So, if our number grows by 50% then our computation grows by 50%
This is linear and can be shown as O(N)
No, we leave out constants because we are not trying to get an exact time measurement. We are only trying to see how our algorithm grows based on time and inputs.
Theoretically O(N^2) is a lot slower than something like O(N) But when it's put into practice O(N^2) can sometimes be faster if your N is small enough.
Take for example insertion sort which is theoretically slower than quicksort but when used with a small enough dataset it is actually faster.
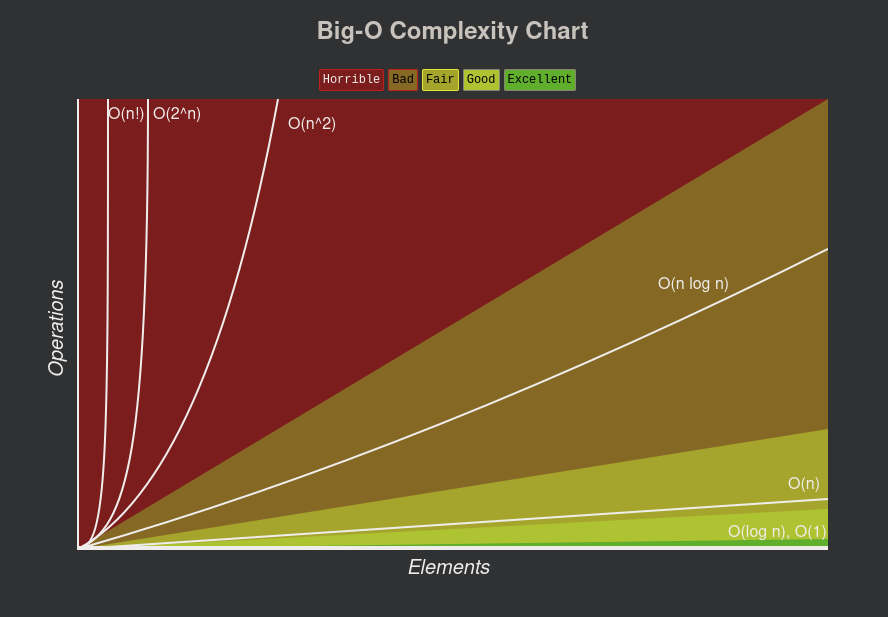
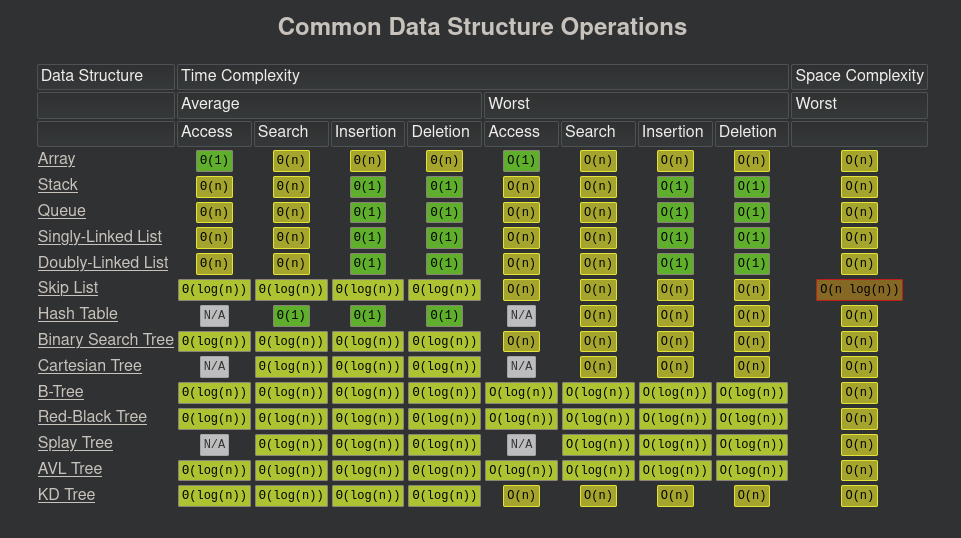
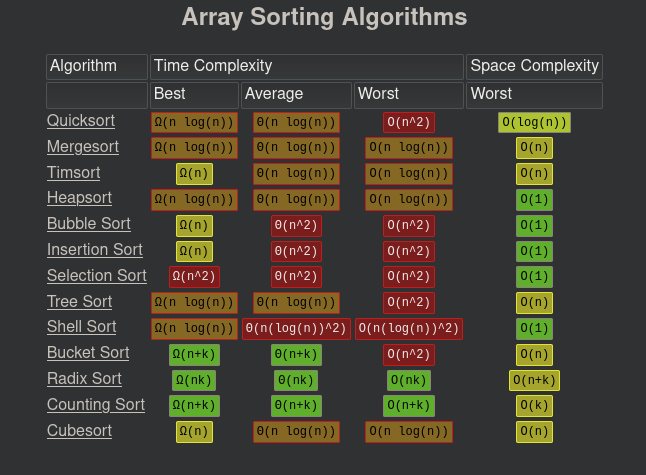
Charts: https://www.bigocheatsheet.com
An array is an unbreaking memory space that contains a certain amount of bytes
When inserting a value into an array it overwrites that specific location in memory with your value.
Due to this unbreaking memory space you cannot grow an array because if you could you might overwrite data in the section of memory you are trying to grow the array into.
Due to an array always having a value at each position this is where null comes in. Null is the ultimate zeroth value an gives the ablility to tell your program that this certin position contains nothing
You always know the position of the value in the array. This means that you do not have to "walk" or loop over each value in the array to get to the place you are trying to go. So, the Big O of insertion and deletion of a value in an array is constand time or O(1)
Constant time does not grow with input at all
constant a = []; an array?Well it's not an array and we call tell it is not an array because we have things like .push where we can grow this "array" infinitly.
So we can say that something is probably happening on top of an array at least and there may be an array underneath the hood but it itself is not an array.
Something more is happening then it being a true array to be able to delete from or add to.
In a true array if you delete index 0, index 0 is still there but it's value just becomes null.
A linear search goes to each value in an array and checks to see if it matches what you are looking for
The worst case of this algorithm is having to search each value in the entire array and not finding the answer
This would make this algorithm O(N). Which is your computation grows at the same rate as the amount of inputs you give it
func search(arr array, answer int) bool {
for (i = 0; i < array.length, i++) {
if (arr[i] === answer) {
return true
}
}
return false
}What if you know that your array is ordered? You can so binary search If you know your array is ordered you can start your seach at the middle of the array and check whether the value is higher or lower. Next you can keep halving it until you reach your value.
Hi is exclusive Low is inclusive
func search(arr array, answer int) bool {
lo := 0
hi := arr.length()
while(low < hi) {
middle := lo + (hi - lo) / 2
value := arr[middle]
if value === answer {
return true
} else if (value > answer) {
hi = middle;
} else {
low = middle + 1
}
}
return false
}If the input halves at each step, it is most likely O(LogN) or O(NlogN)
Given two crystal balls that will break if dropped from a high enough point, determine the exact spot in which it will break in the most optimized way.
Linear Search would work but would not be the most optimized. Keep in mind that we are given two crystal balls. Because this is just a basic linear search we should just know that it is O(N)
Binary Search would also work but again would not be the most optimized. If the first value in the binary search break the ball then we would have to linear search from the beginning to that point because we only have one ball left. This method would be O(1/2N). But we generalized these algoithms. So we drop the constand and it becomes O(N).
To solve this we need to jump by a different unit other than one by one or half by half.
Let's do it by jumping by the sqrt of N. We are going to jump by the sqrt of the array until it breaks. Then we can walk back to our last know good location and linear search from there. Doing this we at most are only going to walk forward by the sqrt of N. That would mean that the running time of this algorithm is O(sqrt(N) + sqrt(N)) We then generalized and this would make this algorithm just O(sqrt(N))
func crystal_balls(floors bool[]) int {
jumps := Math.sqrt(floors.length)
i := jumps
for(_; i < floors.length; i += jumps) {
if (floors[i]) {
return
}
}
i -= jumps
for (j := 0; j < jumps && i < floors.length; ++j) {
if (floors[i]) {
return i;
}
}
return -1;
}Bubble sort is probably the easiest sorting algoritm to learn
Bubble sort works by comparing adjacent elements in an array and swapping their positions if the left element is greater (or smaller for descending order) than the right element. It repeats this process for each pair of adjacent elements until no more swaps are needed.
The condition for swapping two adjacent elements is Xi > Xi+1 or Xi < Xi+1 for decending order.
The worst case time complexity for bubble sort is O(n^2)
This makes bubble sort bad for large dataset but can still be useful for smaller datasets.
func bubble_sort(arr array) array {
for(i = 0; i < arr.length(); ++i) {
for(j = 0; j < arr.length - 1 - i; ++j) {
if (arr[j] > arr[j+1]) {
tmp := arr[j]
arr[j] = arr[j+1]
arr[j+1] = tmp
}
}
}
}